ミンコフスキー空間とローレンツ変換【特殊相対性理論】
当サイトでは、第三者配信の広告サービス(Googleアドセンス)を利用しております。
本記事の内容
本記事では、ミンコフスキー時空図とローレンツ変換について解説しています。
- 4次元時空
- ローレンツ変換の幾何学的解釈
- ローレンツ不変量
- ローレンツ収縮・時間の遅れ
〈関連記事〉
ローレンツ変換については、こちらの記事で詳しく解説しています。
ローレンツ変換の使い方【特殊相対性理論】
4次元時空とローレンツ変換
特殊相対性理論におけるローレンツ変換は、以下で表されます。
ただし、
この式で重要なのは、時間と空間座標が混合しているということです。
このことから、ミンコフスキー(Minkowski)は、空間座標
その空間はミンコフスキー時空と呼ばれます。
ミンコフスキー時空内の1点

ローレンツ不変量と距離
以下で定義される量は、ローレンツ変換に対して値を変えないローレンツ不変量になっています。
実際にローレンツ変換の式を代入することで、確かめてみましょう。
したがって、確かにローレンツ不変量になっていることが分かります。
もし、
このことから、
ミンコフスキー時空図
以下では便宜上、
ミンコフスキー時空図では、横軸を空間
しかし、4次元を図示することはできないため、通常は
ここで、原点から発射した光の世界線について考えると、傾き
物体は光の速度を超えないので、物体の世界線は、
円錐は光円錐(light-cone)と呼ばれます。

ローレンツ変換の幾何学的解釈
まず、
となり、傾き
同様に、
となり、
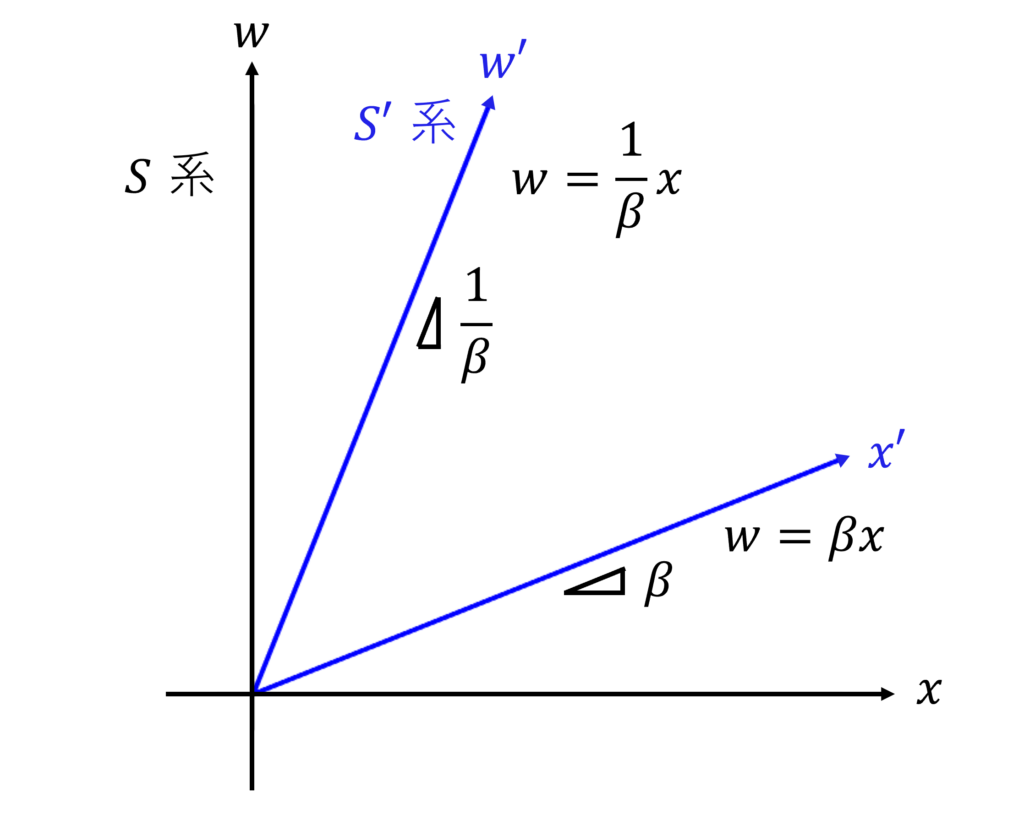
ミンコフスキー時空における単位格子
まず、
これを解いて
が得られます。
同様に、
これを解いて
が得られます。
これを図示すると、以下のようになります。
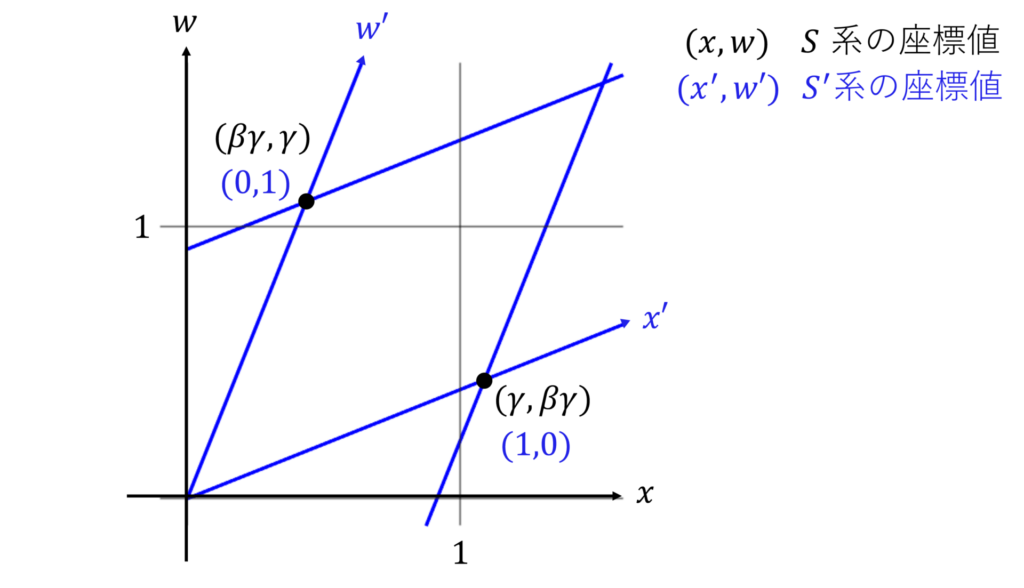
ユークリッド平面で描くと、それぞれの単位長さは異なって見えます。しかし、これはミンコフスキー時空における距離の定義が異なるためです。
ローレンツ収縮
ミンコフスキー時空図でローレンツ収縮を幾何学的に解釈してみましょう。
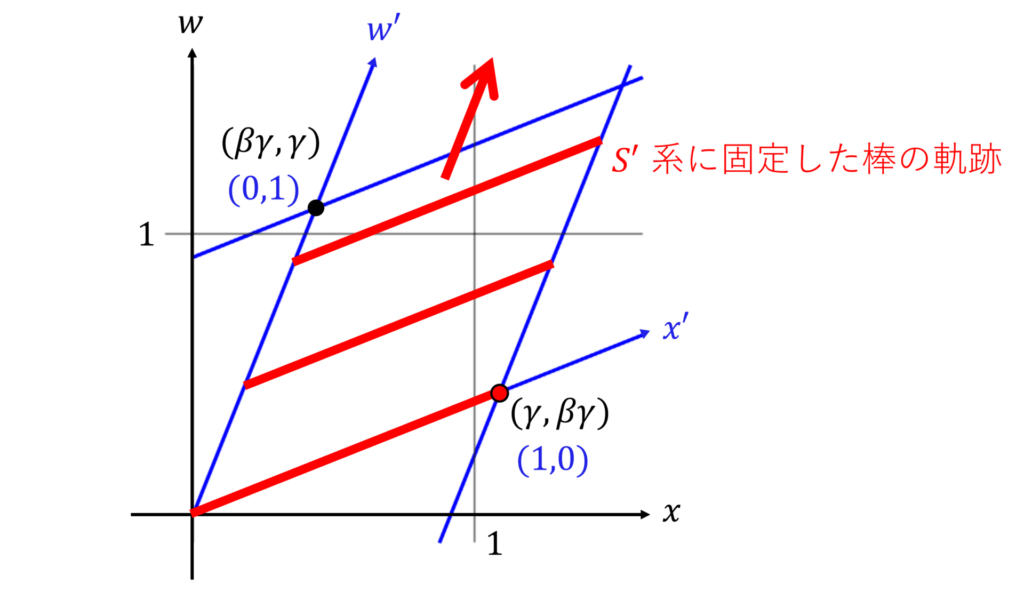
棒の長さ
この棒を
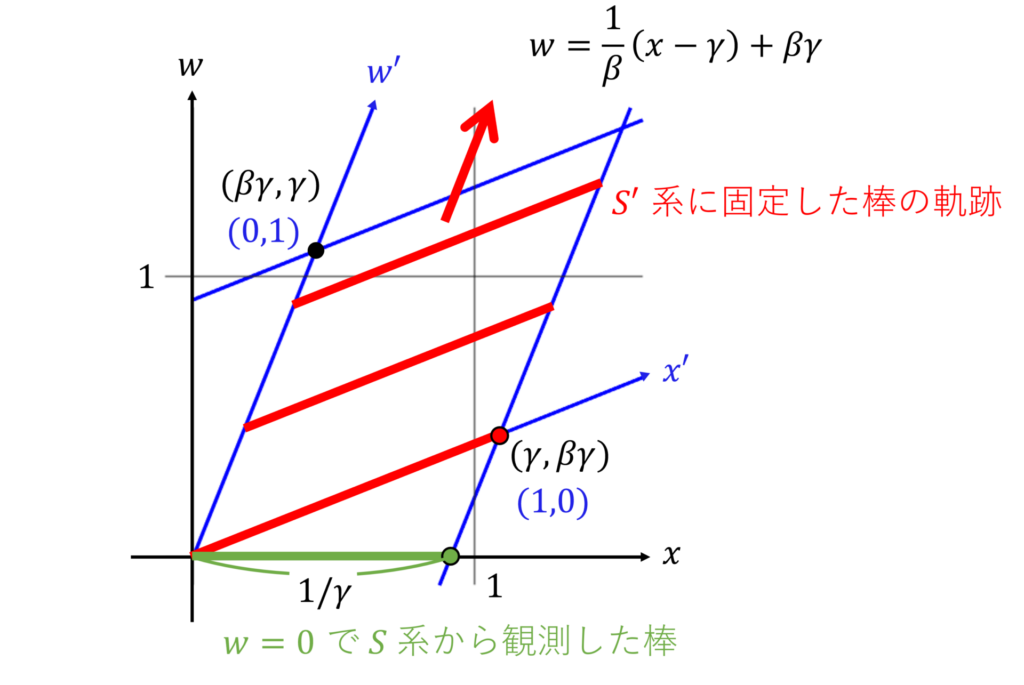
図より、
具体的に端点の座標を求めると、
つまり、
次は逆に、
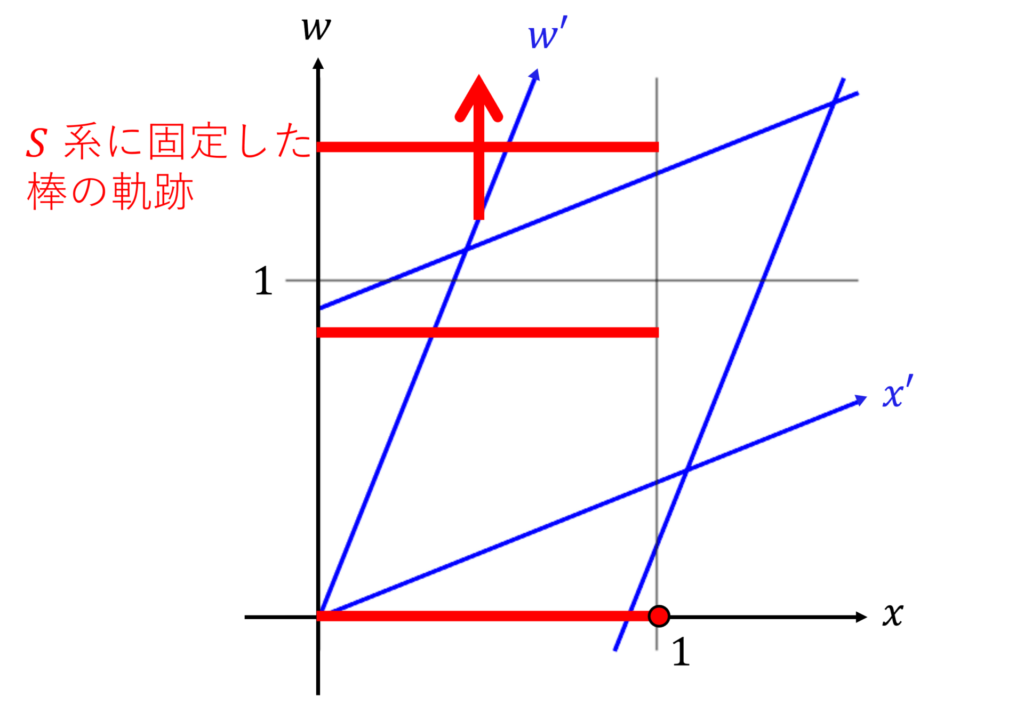

図より、
棒の端点の
ローレンツ変換の式より、
となり、
時間の遅れ
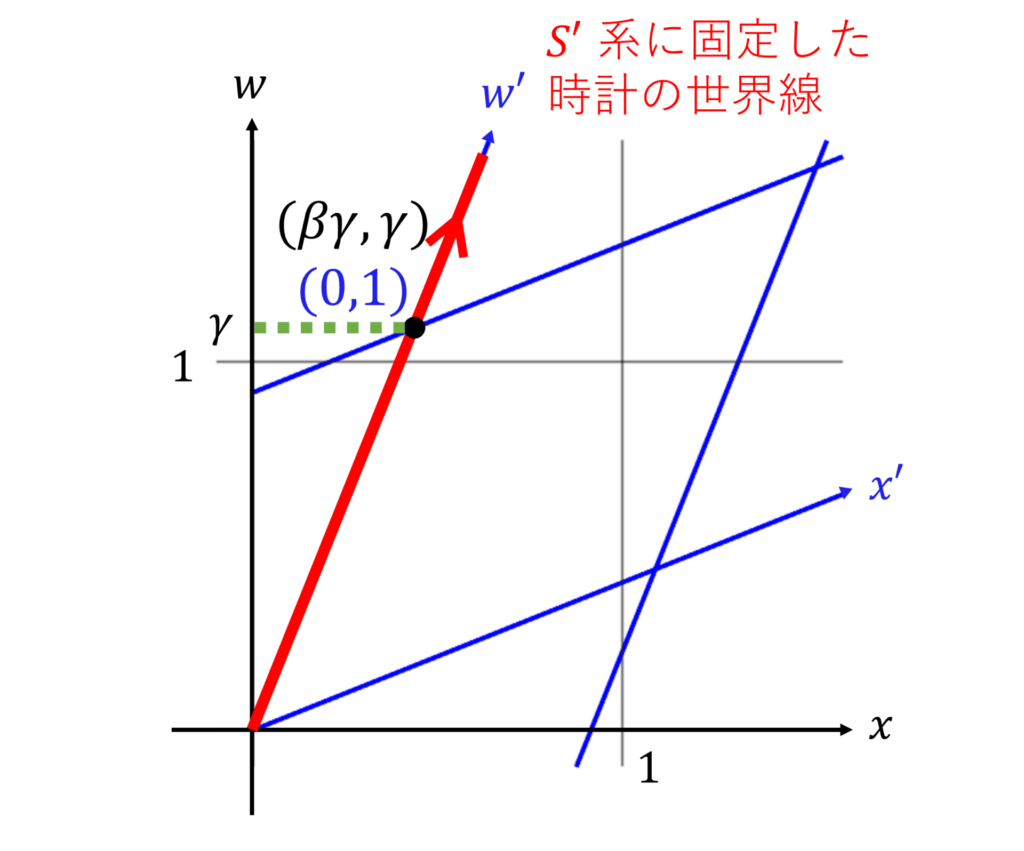
図の赤線が、時計の世界線になります。
先ほど求めた単位格子より、
したがって、動いている時計が、静止している時計に比べて遅れていることが分かります。
逆に、
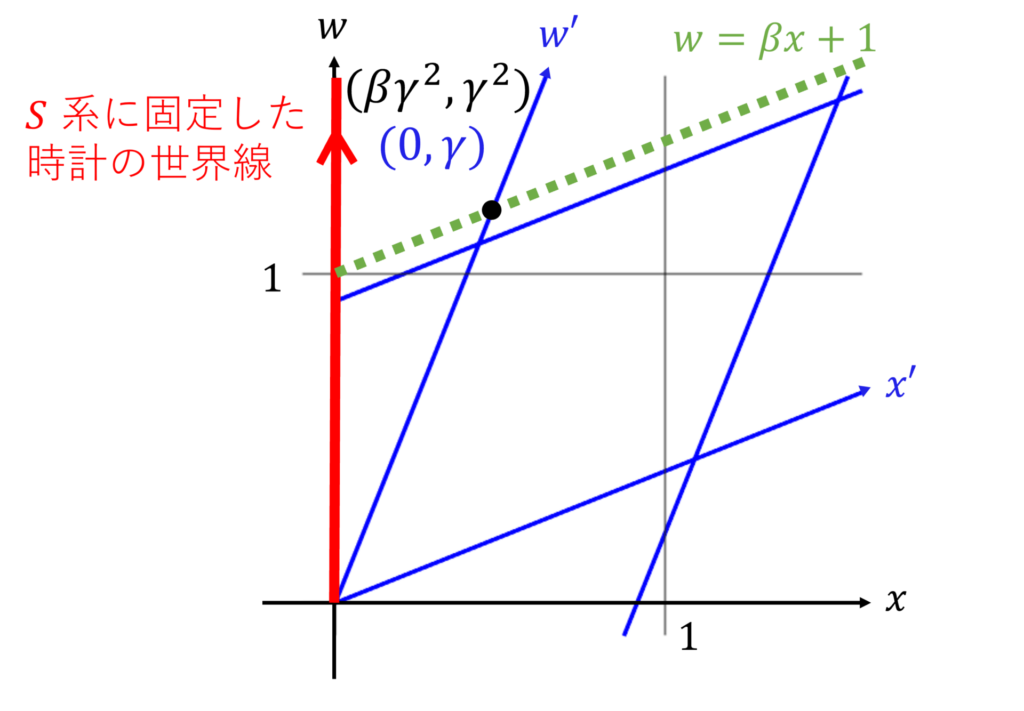
交点の
これをローレンツ変換の式に代入して、
したがって、先ほどと同様に、
参考文献
- 風間洋一(1997)『相対性理論入門講義』培風館


0 件のコメント:
コメントを投稿