【何人必要?】『三体』の人列コンピュータを設計する!ところが…
明けましておめでとうございます.18のhiraです.
僕はコンピュータ工学をやっているつもりなのですが,近年は1つのプロセッサの性能向上が限界に達しつつあり,代わりにマルチコアだったり,AIや行列計算用の専用プロセッサを組み合わせることが主流となっています.
ところが専用プロセッサは少量他品種であり,そのために複雑な回路を設計することは今まで困難でした.
ここに現れたのがGoogleが後援するOpenMPWプログラムです.これはGoogleColab上でDSLXというVerilog(回路のプログラミング)っぽい言語でコードを書くと,それが実際のカスタムプロセッサに変換され,さらに提携しているファブで製造までされるという企画です!しかも内部表現としてXORなどの論理演算の数や,その演算同士のつながりのグラフが得られます.
(設計にはこちらのOpenMPWチュートリアルを参考にしました)
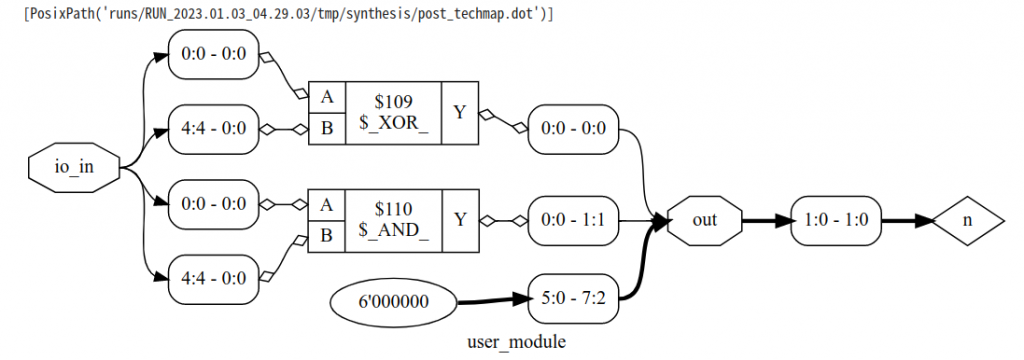
となればやりたいことは1つですね.『三体』の人海戦術の手旗信号による人列コンピュータには何人必要か.三体問題専用プロセッサを作って検証してみましょう!

この記事で作製したMATLABファイル,GoogleColabのipynbファイルはリンクのGithubにありますのでご参照ください.
(注: 以下の記事には『三体』のネタバレを含みます)

三体星人が困りに困っていたように,3つ以上の星が相互に重力を及ぼし合って運動する軌道は一般解をもたず,複雑極まりない軌道をすることが知られています.しかし恒星が近づいては灼熱地獄,遠ざかっては絶対零度という環境のため,星の軌道を予測して地下に避難する必要がありました.
そんな三体問題ですが,完璧な解は求まらなくても,数値的に「ある程度正しい」解は求めることができます.ざっくり言うと現時点の星の座標と速度,重力から,微小時間後の座標を求めることを繰り返し,未来の軌道を求めます.
「数値解析」という学問で,同じような計算をコンピュータでガンガン繰り返しまくります.
Symplectic法による天体運動の数値解析
数値解析の方法としては,ルンゲクッタ法など色々ありますが,今回はSymplectic法を用いました.といっても高校の天体物理に毛が生えた程度です.
Symplectic法は以下の流れで数値計算を行います.ここで を座標( , , ), を速度, を恒星( , , )の質量とし,重力定数 は として無視します.また天体は2次元円盤上を動くとして 座標は無視します.天体 の1ステップ後の 座標 , 方向の速度 は次のようになります.
この新しい , をを各天体の各座標ごとに求めます.
これをMATLABで実装したものがsymp_test.mです.試しに「8の字軌道」と知られている安定解を入れてみたところ,0.0001秒刻みでの0.0~20.0sまでの軌道は次のようになりました.
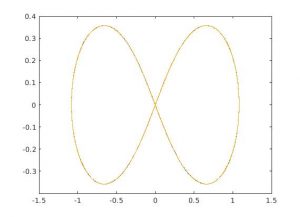
確かに8の字が求まっています!このSymplectic法のアルゴリズムをOpenMPWでカスタムプロセッサの回路にします.
三体問題専用のカスタムプロセッサの作製
皆様がお持ちのパソコンやスマートフォンに入っているIntelとかのチップは「汎用プロセッサ」と呼ばれるもので,プログラム次第で電卓,ゲーム,文書作製となんでもできます.この内部には加算器,乗算器,分岐器,小数点計算器などたくさんの回路があり,プログラムは「この値を加算しろ.その結果に応じてプログラムのN行目に移動しろ」などと命令しています.加算器などの「小道具」みたいな回路がたくさんあり,それを使う順番や与える値を指定する超長くて細かい指示書がプログラムと言えます.多くの種類の小道具を持っていますが,基本的に1つの道具は1個しか持っていないため,「乗算を100回行う」といった場合には1個の乗算器だけで100回演算を繰り返す必要があります.
これに対しカスタムプロセッサは特定の回路しかもちません.加算器しか持たないカスタムプロセッサは加算しかできません.しかし不必要な回路がないため低消費電力だったり,反対に加算器を100万個並列にすれば100万回の加算が一度にできます.これは画像処理など数百万のピクセル1つ1つに同じ演算を行いたい場合には非常に効率的で,テレビ内蔵の専用プロセッサといった特定用途では素晴らしい効果を発揮できます.
汎用にしろカスタムにしろ,加算器などその内部はORやANDと呼ばれる極小の論理演算を組み合わさったものという点では同じです.『三体』の旗振り人が無数に並んでいるイメージです.
三体星人もこれを真似して,XORの人,ANDの人,ORの人,…とかいうように人を割り当てて,人海戦術の論理演算手旗信号で自分たちがコンピュータそのものとなって,三体問題を計算したのでした.
もちろん,汎用プロセッサを作ってその上で三体問題"プログラム"を走らせれば同じ結果は得られますし,プログラム次第で国家予算の計算もできます.しかしプロセッサに合わせてプログラムを作る必要があり,どうしても冗長と無駄が発生していまいます.文明崩壊という事態の重大性を鑑みて,今回は三体問題用のカスタムプロセッサを作ってとにかく速く計算することを目指します.
OpenMPWでは,例えば2つの32bitの数a,bを加算する極小加算器のカスタムプロセッサを次のように記述することで作製できます.
fn adder(a: u32, b: u32) -> u32 { let addResult: u32 = a + b; addResult }
引数として与えられた2つの32bit数を足して1つの32bit数として出力しています.これが論理演算に変換されると,ページ冒頭のようなXORやANDのがつながった回路図のようになります(図では1bit同士の加算).
MATLABで作製したSymplectic法のコードをそっくりそのまま,この記法で記述します.冒頭の参考Githubのthree_body_processor.ipynbがこれで,GoogleColab上で実行します.
sqrt()などが必要ですが,DSLXではまだ浮動小数の計算が整備途中なようでしたので,DSLXのコンパイラである「XLS」の開発Githubにあったサポートチームが作成したsqrt()などを使いました.
, から を求めるDSLX記述は次のようになります.
let aqSubBqX: F32 = apfloat_sub_2::apfloat_sub_2<u32:8, u32:23>(aqx, bqx); let aqSubBqX2: F32 = apfloat_mul_2::apfloat_mul_2<u32:8, u32:23>(aqSubBqX, aqSubBqX); let aqSubBqY: F32 = apfloat_sub_2::apfloat_sub_2<u32:8, u32:23>(aqy, bqy); let aqSubBqY2: F32 = apfloat_mul_2::apfloat_mul_2<u32:8, u32:23>(aqSubBqY, aqSubBqY); let rab2: F32 = apfloat_add_2::add<u32:8, u32:23>(aqSubBqX2, aqSubBqY2); let rab: F32 = fpsqrt_32(rab2); let rab3: F32 = apfloat_mul_2::apfloat_mul_2<u32:8, u32:23>(rab, rab2);
同じように の計算や の計算を行う回路を記述し,各天体,各座標ごとに結果を求めます.
ここで,引数に応じて回路を2天体 , の距離( )を求める回路と,それを用いて新しい 軸方向の座標・速度( )を求める回路に分割します.これには次の理由があります.
- 与える数値が違うだけで,各軸ごとの計算は同じ
- 回路規模の大きい乗算器などをいっぱい使うため,とりあえず最小の1セットを作る
- 満艦飾でやってみたが,GoogleColabのRAMをオーバーしてしまった
引数に応じて, 回路は , , を求め, 回路は , ,…, を求めます.
冒頭のチュートリアルを参考に,記述した回路を論理回路の図にする際に.dotファイルが生成されます.これは論理演算の繋がりをグラフ構造にしており,このファイルをダウンロード(Colab横のリソースタブなどから可)して中のXORとかの数を数えます.
ちなみに調子に乗ってグラフを図にしようとしたところ,とんでもなく重くて5時間経っても計算が終わりませんでした.
とりあえずfloat減算1行だけの演算の内部構造を図にしてみました.(これだけで20分近くかかった気がする)
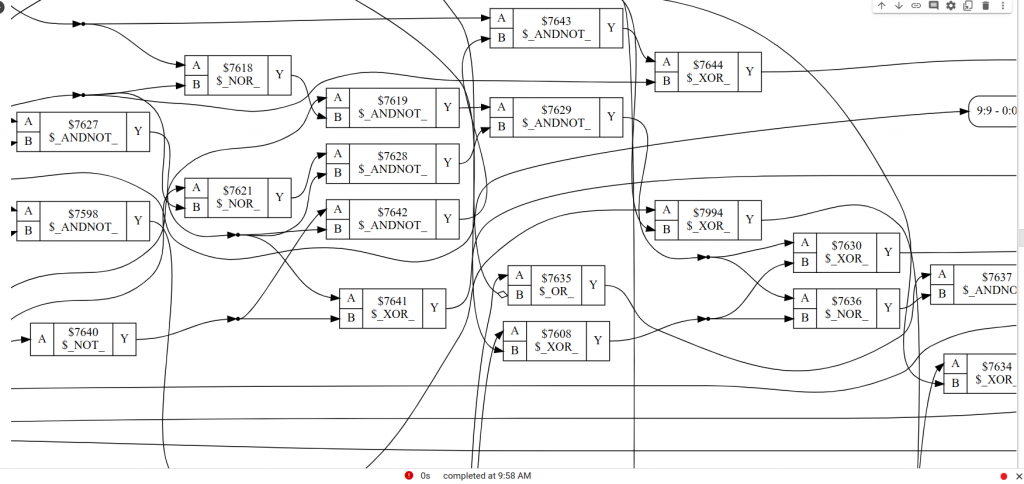
さて, 回路と をそれぞれ作製しました.それらに使われているOR,NOTOR,AND,NOTAND,XOR,NOR,XNOR,MUX(マルチプレクサ)の個数を数えた結果が以下の表です.
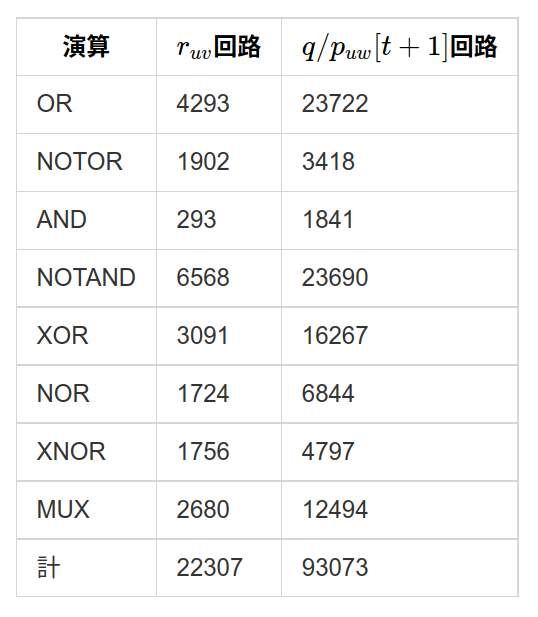
これより約12万人いれば天体間の距離の計算と新しい位置・速度の計算ができます.ただ,これが1つずつだと と , の計算が1回に1つしかできず,同様に6種ある も1つずつしか行えません.
そのため全部を一度に行うには 回路を3つ, 回路を6つ並列させる必要があります.この場合,必要な人員は約63万人となります.とはいえ無理なことではないでしょう.かの赤壁の戦いでは曹操軍は80万で侵攻したとも言われています.もちろん膨大な支援要員も必要ですが,1人1人がやることは前の人の旗に応じて自分の旗を上げるだけの,それこそ子供も5分で覚えられることです.戦闘なんて高度で人的消費の激しいこともしないのですから,農作業を免除して町一つ徴用すれば余裕で事足ります.むしろ暇すぎるくらい.
めでたしめでたし,のはずが…
これで,三体文明は救われますね!8の字解もきちんと求まりました.暇ですから,「ピタゴラス三体問題」でも解いてみましょう.
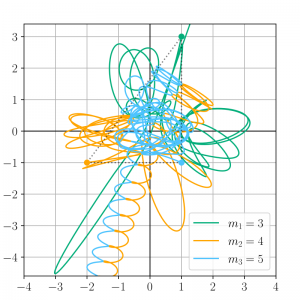
ピタゴラス三体問題は星の質量比が3:4:5になっていて,初期状態の位置が辺の比が3:4:5の直角三角形の頂点上にある場合の三体問題です.冒頭の摩訶不思議な軌道の図がコレの数値解です.
作製したsymplectic法のMATLABコードに,0.0~15.0sまでのピタゴラス三体問題を実行させてみると次のようになりました.左がWikiにあった「正解」の軌道で,右がMATLABコードで試してカスタムプロセッサ化した自作の軌道です.
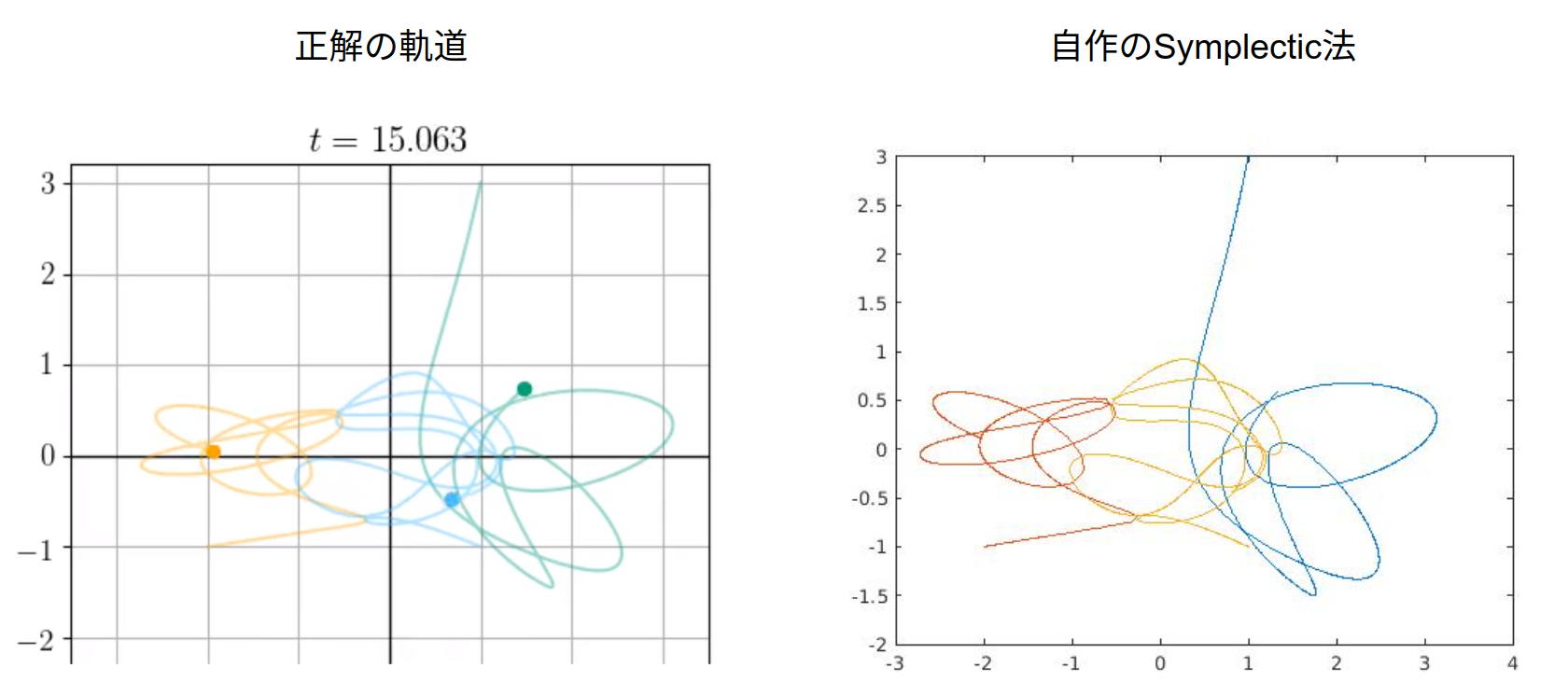
良いですね,なかなか正確では!?これで三体文明は安泰です!
と,気を緩めて16.0sまでやってみたところ,問題が発生しました.
右の自作数値計算では2つの星が画面外に飛び出してしまっています!つまり計算が間違っています!
一体ナゼこのようなことになってしまったのでしょうか…その答えはt=15.830の時にありました.
t=15.830近辺において,2つの星が非常に接近しています.これにより に反比例する力の変異が急になりすぎて計算精度が追いつかないという問題が発生してしまいました…当然,以降の計算結果はおかしくなります.
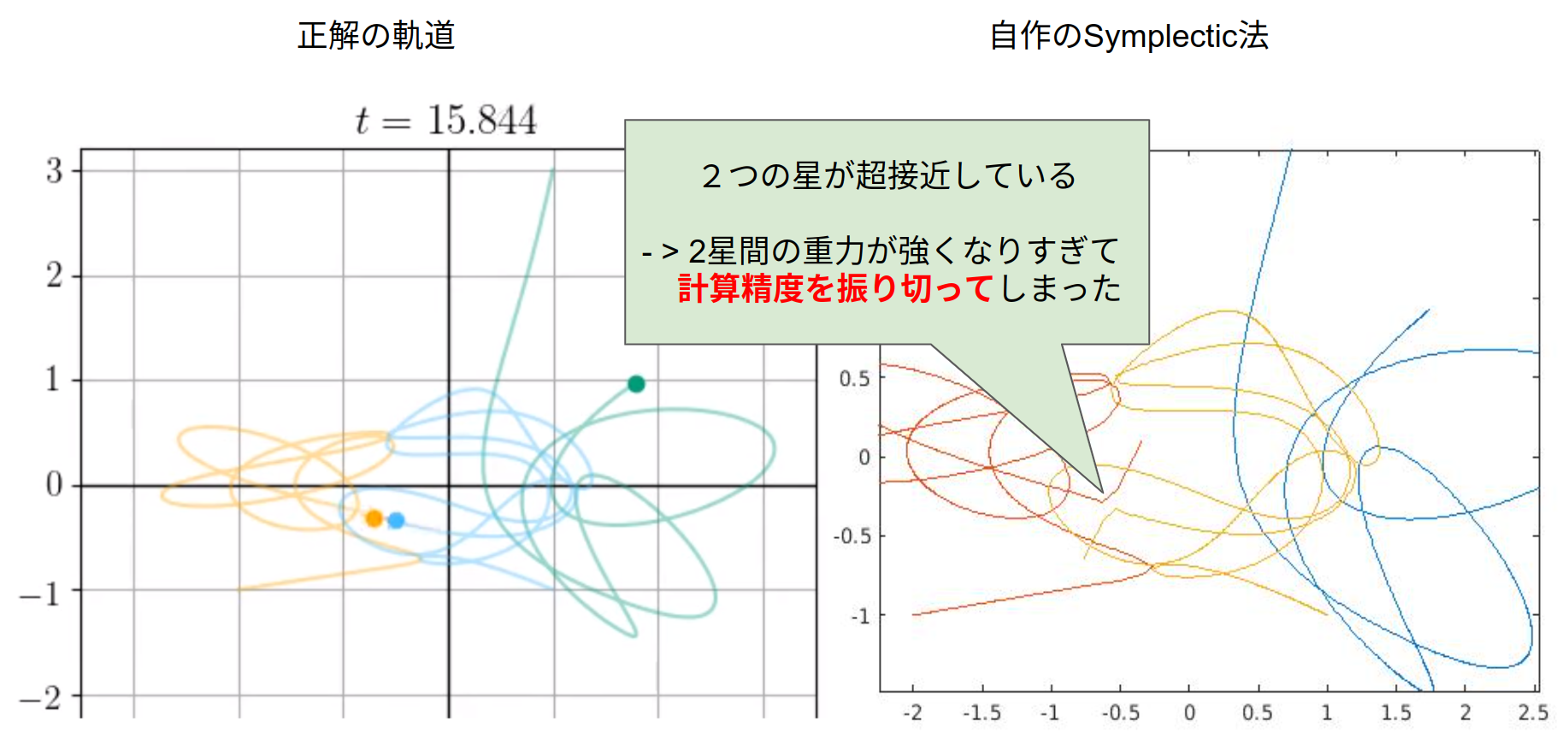
これでは三体文明が崩壊してしまいます.どうするべきでしょうか…?
どうにかするための3つの道
1. 256bitなど高精度コンピュータにする
私達が使っているPCやスマホの多くは64bitで1つの数字を表しています.また車載やIoTといった小型コンピュータは32bitで1つの数字を表しています.つまり精度に限界があり,32bitだと一般に7桁の精度が限界と言われています.
これを128bitとか256bitとかに増やしていけばその分小さい数まで表せるので小さい数を見逃すことがなくなり,精度は高まります.一方で消費電力やメモリの使用量は増加します.
2. アルゴリズムのステップ幅を工夫する (正解)
今回のシミュレーションでは常に同じステップ幅 で時間を経過させてきました.そのためかかっている力が大きい時は, の間に遠くまで飛んでいってしまいます.ただしステップ時間が小さいと計算に時間がかかり過ぎ,さらに不当に小さすぎるとかえって計算結果がおかしくなってしまうことが知られています.
そのため力にあわせて,常に「丁度良い距離」だけ動くようにステップ時間を変化させることが有効です.おそらくこれが正解の道なのですが,もちろんステップ時間計算とう処理が加わるためアルゴリズムは複雑になります.
3. 小説として面白いからこれで良い.("何もせんほうがええ")
三体文明には死んでもらいます.これによって『三体』のあの人列コンピュータのシーンはたぶん面白くなります.
この場合のシナリオは次のようになるでしょう.
(最初のうまくいっている時)
ニュートン&ノイマン「Symplectic法による三体問題計算機が出来ました!」
始皇帝「すごい,今のところ完璧に一致している!よく励めよ!」
(接近エラーが起きて2星が飛んでいった時)
ニ&ノ「吉報です!2星が最接近した後,宇宙の彼方へ飛んでいきます!これで残った恒星は1つになり,1恒星1惑星の安定した軌道になります!皇帝の徳の賜物です!」
帝「まさに天佑だ!これで我が文明は苦しみから永遠に解放される!貴様らの大功をもってニュートンを丞相に,ノイマンを征星大将軍とする!せっかくだから秦を改元して"完"とでもしよう!」
(完歴N年,計算間違いの発覚)
帝「おかしいな,接近はしたけどまだ星が3つとも残っているぞ?」
ニ&ノ「そんなはずは…なにか間違いでもあったのか?」
(完歴N年,手遅れの瞬間)
ニ&ノ「ごめんなさい,間違っていました!星が接近するとコンピュータの精度を振り切って計算が失敗してしまいます.(グラグラ)おや,こんな時に地震か…?」
悪くないのでは?
おわりに
18#hiraは計算精度のオーバーフローで諦めました.この人は初等の数値計算レベルまで到達していました.長い時間のあと,気力と学力がいまいちど勃興し,『三次元』の予測不能の世界で,ふたたび進歩をはじめることはないでしょう.



0 件のコメント:
コメントを投稿